Portal:Mathematics

Abacus, a ancient hand-operated calculating.
Portrait of Emmy Noether, around 1900.
Euler's identity

Mathematics is a field of study that discovers and organizes methods, theories and theorems that are developed and proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). (Full article...)

Featured articles

Image 1

Noether c. 1900–1910

Amalie Emmy Noether (US: /ˈnʌtər/, UK: /ˈnɜːtə/; German: [ˈnøːtɐ]; 23 March 1882 – 14 April 1935) was a German mathematician who made many important contributions to abstract algebra. She proved Noether's first and second theorems, which are fundamental in mathematical physics. She was described by Pavel Alexandrov, Albert Einstein, Jean Dieudonné, Hermann Weyl and Norbert Wiener as the most important woman in the history of mathematics. As one of the leading mathematicians of her time, she developed theories of rings, fields, and algebras. In physics, Noether's theorem explains the connection between symmetry and conservation laws.

Noether was born to a Jewish family in the Franconian town of Erlangen; her father was the mathematician Max Noether. She originally planned to teach French and English after passing the required examinations but instead studied mathematics at the University of Erlangen, where her father lectured. After completing her doctorate in 1907 under the supervision of Paul Gordan, she worked at the Mathematical Institute of Erlangen without pay for seven years. At the time, women were largely excluded from academic positions. In 1915, she was invited by David Hilbert and Felix Klein to join the mathematics department at the University of Göttingen, a world-renowned center of mathematical research. The philosophical faculty objected, however, and she spent four years lecturing under Hilbert's name. Her habilitation was approved in 1919, allowing her to obtain the rank of Privatdozent. (Full article...)
Image 2
Logic studies valid forms of inference like modus ponens.

Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the study of deductively valid inferences or logical truths. It examines how conclusions follow from premises based on the structure of arguments alone, independent of their topic and content. Informal logic is associated with informal fallacies, critical thinking, and argumentation theory. Informal logic examines arguments expressed in natural language whereas formal logic uses formal language. When used as a countable noun, the term "a logic" refers to a specific logical formal system that articulates a proof system. Logic plays a central role in many fields, such as philosophy, mathematics, computer science, and linguistics.

Logic studies arguments, which consist of a set of premises that leads to a conclusion. An example is the argument from the premises "it's Sunday" and "if it's Sunday then I don't have to work" leading to the conclusion "I don't have to work". Premises and conclusions express propositions or claims that can be true or false. An important feature of propositions is their internal structure. For example, complex propositions are made up of simpler propositions linked by logical vocabulary like $\land$ (and) or $\to$ (if...then). Simple propositions also have parts, like "Sunday" or "work" in the example. The truth of a proposition usually depends on the meanings of all of its parts. However, this is not the case for logically true propositions. They are true only because of their logical structure independent of the specific meanings of the individual parts. (Full article...)
Image 3
Plots of logarithm functions, with three commonly used bases. The special points $log b b = 1$ are indicated by dotted lines, and all curves intersect in $log b 1 = 0$ .

In mathematics, the logarithm to base $b$ is the inverse function of exponentiation with base $b$ . That means that the logarithm of a number $x$ to the base $b$ is the exponent to which $b$ must be raised to produce $x$ . For example, since $1000 = 10 3$ , the logarithm base $10$ of $1000$ is $3$ , or $log 10 (1000) = 3$ . The logarithm of $x$ to base $b$ is denoted as $log b (x)$ , or without parentheses, $log b x$ . When the base is clear from the context or is irrelevant it is sometimes written $log x$ .

The logarithm base $10$ is called the decimal or common logarithm and is commonly used in science and engineering. The natural logarithm has the number $e \approx 2.718$ as its base; its use is widespread in mathematics and physics because of its very simple derivative. The binary logarithm uses base $2$ and is frequently used in computer science. (Full article...)
$Image 4 Euclid's method for finding the greatest common divisor (GCD) of two starting lengths BA and DC, both defined to be multiples of a common "unit" length. The length DC being shorter, it is used to "measure" BA, but only once because the remainder EA is less than DC. EA now measures (twice) the shorter length DC, with remainder FC shorter than EA. Then FC measures (three times) length EA. Because there is no remainder, the process ends with FC being the GCD. On the right Nicomachus's example with numbers 49 and 21 resulting in their GCD of 7 (derived from Heath 1908:300). In mathematics, the Euclidean algorithm, or Euclid's algorithm, is an efficient method for computing the greatest common divisor (GCD) of two integers, the largest number that divides them both without a remainder. It is named after the ancient Greek mathematician Euclid, who first described it in his Elements (c. 300 BC). It is an example of an algorithm, a step-by-step procedure for performing a calculation according to well-defined rules, and is one of the oldest algorithms in common use. It can be used to reduce fractions to their simplest form, and is a part of many other number-theoretic and cryptographic calculations. The Euclidean algorithm is based on the principle that the greatest common divisor of two numbers does not change if the larger number is replaced by its difference with the smaller number. For example, 21 is the GCD of 252 and 105 (as 252 = 21 × 12 and 105 = 21 × 5), and the same number 21 is also the GCD of 105 and 252 − 105 = 147. Since this replacement reduces the larger of the two numbers, repeating this process gives successively smaller pairs of numbers until the two numbers become equal. When that occurs, that number is the GCD of the original two numbers. By reversing the steps or using the extended Euclidean algorithm, the GCD can be expressed as a linear combination of the two original numbers, that is the sum of the two numbers, each multiplied by an integer (for example, 21 = 5 × 105 + (−2) × 252). The fact that the GCD can always be expressed in this way is known as Bézout's identity. (Full article...)$

Image 4
Euclid's method for finding the greatest common divisor (GCD) of two starting lengths BA and DC, both defined to be multiples of a common "unit" length. The length DC being shorter, it is used to "measure" BA, but only once because the remainder EA is less than DC. EA now measures (twice) the shorter length DC, with remainder FC shorter than EA. Then FC measures (three times) length EA. Because there is no remainder, the process ends with FC being the GCD. On the right Nicomachus's example with numbers 49 and 21 resulting in their GCD of 7 (derived from Heath 1908:300).

In mathematics, the Euclidean algorithm, or Euclid's algorithm, is an efficient method for computing the greatest common divisor (GCD) of two integers, the largest number that divides them both without a remainder. It is named after the ancient Greek mathematician Euclid, who first described it in his Elements (c. 300 BC).
It is an example of an algorithm, a step-by-step procedure for performing a calculation according to well-defined rules,
and is one of the oldest algorithms in common use. It can be used to reduce fractions to their simplest form, and is a part of many other number-theoretic and cryptographic calculations.

The Euclidean algorithm is based on the principle that the greatest common divisor of two numbers does not change if the larger number is replaced by its difference with the smaller number. For example, $21$ is the GCD of $252$ and $105$ (as $252 = 21 \times 12$ and $105 = 21 \times 5)$ , and the same number $21$ is also the GCD of $105$ and $252 - 105 = 147$ . Since this replacement reduces the larger of the two numbers, repeating this process gives successively smaller pairs of numbers until the two numbers become equal. When that occurs, that number is the GCD of the original two numbers. By reversing the steps or using the extended Euclidean algorithm, the GCD can be expressed as a linear combination of the two original numbers, that is the sum of the two numbers, each multiplied by an integer (for example, $21 = 5 \times 105 + (-2) \times 252$ ). The fact that the GCD can always be expressed in this way is known as Bézout's identity. (Full article...)
Image 5
High-precision test of general relativity by the Cassini space probe (artist's impression): radio signals sent between the Earth and the probe (green wave) are delayed by the warping of spacetime (blue lines) due to the Sun's mass.

General relativity is a theory of gravitation developed by Albert Einstein between 1907 and 1915. The theory of general relativity says that the observed gravitational effect between masses results from their warping of spacetime.

By the beginning of the 20th century, Newton's law of universal gravitation had been accepted for more than two hundred years as a valid description of the gravitational force between masses. In Newton's model, gravity is the result of an attractive force between massive objects. Although even Newton was troubled by the unknown nature of that force, the basic framework was extremely successful at describing motion. (Full article...)
Image 6
The number π (/paɪ/ ; spelled out as "pi") is a mathematical constant, approximately equal to 3.14159, that is the ratio of a circle's circumference to its diameter. It appears in many formulae across mathematics and physics, and some of these formulae are commonly used for defining π, to avoid relying on the definition of the length of a curve.

The number π is an irrational number, meaning that it cannot be expressed exactly as a ratio of two integers, although fractions such as 22 7 {\displaystyle {\tfrac {22}{7}}} are commonly used to approximate it. Consequently, its decimal representation never ends, nor enters a permanently repeating pattern. It is a transcendental number, meaning that it cannot be a solution of an algebraic equation involving only finite sums, products, powers, and integers. The transcendence of π implies that it is impossible to solve the ancient challenge of squaring the circle with a compass and straightedge. The decimal digits of π appear to be randomly distributed, but no proof of this conjecture has been found. (Full article...)
Image 7

Portrait by Jakob Emanuel Handmann, 1753

Leonhard Euler (/ˈɔɪlər/ OY-lər; German: [ˈleːɔnhaʁt ˈʔɔʏlɐ] , Swiss Standard German: [ˈleɔnhard ˈɔʏlər]; 15 April 1707 – 18 September 1783) was a Swiss polymath who was active as a mathematician, physicist, astronomer, logician, geographer, and engineer. He founded the studies of graph theory and topology and made influential discoveries in many other branches of mathematics such as analytic number theory, complex analysis, and infinitesimal calculus. He also introduced much of modern mathematical terminology and notation, including the notion of a mathematical function. He is also known for his work in mechanics, fluid dynamics, optics, astronomy, and music theory. As a result, Euler has been described as a "universal genius" who "was fully equipped with almost unlimited powers of imagination, intellectual gifts and extraordinary memory".

Euler is regarded as arguably the most prolific contributor in the history of mathematics and science, and the greatest mathematician of the 18th century. Several great mathematicians who produced their work after Euler's death have recognised his importance in the field as shown by quotes attributed to many of them: Pierre-Simon Laplace expressed Euler's influence on mathematics by stating, "Read Euler, read Euler, he is the master of us all." Carl Friedrich Gauss wrote: "The study of Euler's works will remain the best school for the different fields of mathematics, and nothing else can replace it." His 866 publications and his correspondence are being collected in the Opera Omnia Leonhard Euler which, when completed, will consist of 81 quartos. He spent most of his adult life in Saint Petersburg, Russia, and in Berlin, then the capital of Prussia. (Full article...)
Image 8

Josiah Willard Gibbs (/ɡɪbz/; February 11, 1839 – April 28, 1903) was an American scientist who made significant theoretical contributions to physics, chemistry, and mathematics. His work on the applications of thermodynamics was instrumental in transforming physical chemistry into a rigorous deductive science. Together with James Clerk Maxwell and Ludwig Boltzmann, he created statistical mechanics (a term that he coined), explaining the laws of thermodynamics as consequences of the statistical properties of ensembles of the possible states of a physical system composed of many particles. Gibbs also worked on the application of Maxwell's equations to problems in physical optics. As a mathematician, he created modern vector calculus (independently of the British scientist Oliver Heaviside, who carried out similar work during the same period) and described the Gibbs phenomenon in the theory of Fourier analysis.

In 1863, Yale University awarded Gibbs the first American doctorate in engineering. After a three-year sojourn in Europe, Gibbs spent the rest of his career at Yale, where he was a professor of mathematical physics from 1871 until his death in 1903. Working in relative isolation, he became the earliest theoretical scientist in the United States to earn an international reputation and was praised by Albert Einstein as "the greatest mind in American history". In 1901, Gibbs received what was then considered the highest honor awarded by the international scientific community, the Copley Medal of the Royal Society of London, "for his contributions to mathematical physics". (Full article...)
Image 9

One of Molyneux's celestial globes, which is displayed in Middle Temple Library – from the frontispiece of the Hakluyt Society's 1889 reprint of A Learned Treatise of Globes, both Cœlestiall and Terrestriall, one of the English editions of Robert Hues' Latin work Tractatus de Globis (1594)

Emery Molyneux (/ˈɛməri ˈmɒlɪnoʊ/ EM-ər-ee MOL-in-oh; died June 1598) was an English Elizabethan maker of globes, mathematical instruments and ordnance. His terrestrial and celestial globes, first published in 1592, were the first to be made in England and the first to be made by an Englishman.

Molyneux was known as a mathematician and maker of mathematical instruments such as compasses and hourglasses. He became acquainted with many prominent men of the day, including the writer Richard Hakluyt and the mathematicians Robert Hues and Edward Wright. He also knew the explorers Thomas Cavendish, Francis Drake, Walter Raleigh and John Davis. Davis probably introduced Molyneux to his own patron, the London merchant William Sanderson, who largely financed the construction of the globes. When completed, the globes were presented to Elizabeth I. Larger globes were acquired by royalty, noblemen and academic institutions, while smaller ones were purchased as practical navigation aids for sailors and students. The globes were the first to be made in such a way that they were unaffected by the humidity at sea, and they came into general use on ships. (Full article...)
Image 10

Cantor, c. 1910

Georg Ferdinand Ludwig Philipp Cantor (/ˈkæntɔːr/ KAN-tor; German: [ˈɡeːɔʁk ˈfɛʁdinant ˈluːtvɪç ˈfiːlɪp ˈkantoːɐ̯]; 3 March [O.S. 19 February] 1845 – 6 January 1918) was a mathematician who played a pivotal role in the creation of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets, and proved that the real numbers are more numerous than the natural numbers. Cantor's method of proof of this theorem implies the existence of an infinity of infinities. He defined the cardinal and ordinal numbers and their arithmetic. Cantor's work is of great philosophical interest, a fact he was well aware of.

Originally, Cantor's theory of transfinite numbers was regarded as counter-intuitive – even shocking. This caused it to encounter resistance from mathematical contemporaries such as Leopold Kronecker and Henri Poincaré and later from Hermann Weyl and L. E. J. Brouwer, while Ludwig Wittgenstein raised philosophical objections; see Controversy over Cantor's theory. Cantor, a devout Lutheran Christian, believed the theory had been communicated to him by God. Some Christian theologians (particularly neo-Scholastics) saw Cantor's work as a challenge to the uniqueness of the absolute infinity in the nature of God – on one occasion equating the theory of transfinite numbers with pantheism – a proposition that Cantor vigorously rejected. Not all theologians were against Cantor's theory; prominent neo-scholastic philosopher Constantin Gutberlet was in favor of it and Cardinal Johann Baptist Franzelin accepted it as a valid theory (after Cantor made some important clarifications). (Full article...)
Image 11

Rejewski, c. 1932

Marian Adam Rejewski (Polish: [ˈmarjan rɛˈjɛfskʲi] ; 16 August 1905 – 13 February 1980) was a Polish mathematician and cryptologist who in late 1932 reconstructed the sight-unseen German military Enigma cipher machine, aided by limited documents obtained by French military intelligence.

Over the next nearly seven years, Rejewski and fellow mathematician-cryptologists Jerzy Różycki and Henryk Zygalski, working at the Polish General Staff's Cipher Bureau, developed techniques and equipment for decrypting the Enigma ciphers, even as the Germans introduced modifications to their Enigma machines and encryption procedures. Rejewski's contributions included the cryptologic card catalog and the cryptologic bomb. (Full article...)
Image 12

Hilary Putnam

The Quine–Putnam indispensability argument is an argument in the philosophy of mathematics for the existence of abstract mathematical objects such as numbers and sets, a position known as mathematical platonism. It was named after the philosophers Willard Van Orman Quine and Hilary Putnam, and is one of the most important arguments in the philosophy of mathematics.

Although elements of the indispensability argument may have originated with thinkers such as Gottlob Frege and Kurt Gödel, Quine's development of the argument was unique for introducing to it a number of his philosophical positions such as naturalism, confirmational holism, and the criterion of ontological commitment. Putnam gave Quine's argument its first detailed formulation in his 1971 book Philosophy of Logic. He later came to disagree with various aspects of Quine's thinking, however, and formulated his own indispensability argument based on the no miracles argument in the philosophy of science. A standard form of the argument in contemporary philosophy is credited to Mark Colyvan; whilst being influenced by both Quine and Putnam, it differs in important ways from their formulations. It is presented in the Stanford Encyclopedia of Philosophy: (Full article...)
Image 13

Bust of Shen at the Beijing Ancient Observatory

Shen Kuo (Chinese: 沈括; 1031–1095) or Shen Gua, courtesy name Cunzhong (存中) and pseudonym Mengqi (now usually given as Mengxi) Weng (夢溪翁), was a Chinese polymath, scientist, and statesman of the Song dynasty (960–1279). Shen was a master in many fields of study including mathematics, optics, and horology. In his career as a civil servant, he became a finance minister, governmental state inspector, head official for the Bureau of Astronomy in the Song court, Assistant Minister of Imperial Hospitality, and also served as an academic chancellor. At court his political allegiance was to the Reformist faction known as the New Policies Group, headed by Chancellor Wang Anshi (1021–1085).

In his Dream Pool Essays or Dream Torrent Essays (夢溪筆談; Mengxi Bitan) of 1088, Shen was the first to describe the magnetic needle compass, which would be used for navigation (first described in Europe by Alexander Neckam in 1187). Shen discovered the concept of true north in terms of magnetic declination towards the north pole, with experimentation of suspended magnetic needles and "the improved meridian determined by Shen's [astronomical] measurement of the distance between the pole star and true north". This was the decisive step in human history to make compasses more useful for navigation, and may have been a concept unknown in Europe for another four hundred years (evidence of German sundials made circa 1450 show markings similar to Chinese geomancers' compasses in regard to declination). (Full article...)
Image 14

Richard Phillips Feynman (/ˈfaɪnmən/; May 11, 1918 – February 15, 1988) was an American theoretical physicist. He is best known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics, the physics of the superfluidity of supercooled liquid helium, and in particle physics, for which he proposed the parton model. For his contributions to the development of quantum electrodynamics, Feynman received the Nobel Prize in Physics in 1965 jointly with Julian Schwinger and Shin'ichirō Tomonaga.

Feynman developed a widely used pictorial representation scheme for the mathematical expressions describing the behavior of subatomic particles, which later became known as Feynman diagrams. During his lifetime, Feynman became one of the best-known scientists in the world. In a 1999 poll of 130 leading physicists worldwide by the British journal Physics World, he was ranked the seventh-greatest physicist of all time. (Full article...)
Image 15
The first 15,000 partial sums of 0 + 1 − 2 + 3 − 4 + ... The graph is situated with positive integers to the right and negative integers to the left.

In mathematics, 1 − 2 + 3 − 4 + ··· is an infinite series whose terms are the successive positive integers, given alternating signs. Using sigma summation notation the sum of the first m terms of the series can be expressed as
$\sum _{n=1}^{m}n(-1)^{n-1}.$

The infinite series diverges, meaning that its sequence of partial sums, (1, −1, 2, −2, 3, ...), does not tend towards any finite limit. Nonetheless, in the mid-18th century, Leonhard Euler wrote what he admitted to be a paradoxical equation:
$1-2+3-4+\cdots ={\frac {1}{4}}.$ (Full article...)

Good articles

Image 1
A Pythagorean tiling

A Pythagorean tiling or two squares tessellation is a tiling of a Euclidean plane by squares of two different sizes, in which each square touches four squares of the other size on its four sides. Many proofs of the Pythagorean theorem are based on it, explaining its name. It is commonly used as a pattern for floor tiles. When used for this, it is also known as a hopscotch pattern or pinwheel pattern,
but it should not be confused with the mathematical pinwheel tiling, an unrelated pattern.

This tiling has four-way rotational symmetry around each of its squares. When the ratio of the side lengths of the two squares is an irrational number such as the golden ratio, its cross-sections form aperiodic sequences with a similar recursive structure to the Fibonacci word. Generalizations of this tiling to three dimensions have also been studied. (Full article...)
Image 2
A Möbius strip made with paper and adhesive tape

In mathematics, a Möbius strip, Möbius band, or Möbius loop is a surface that can be formed by attaching the ends of a strip of paper together with a half-twist. As a mathematical object, it was discovered by Johann Benedict Listing and August Ferdinand Möbius in 1858, but it had already appeared in Roman mosaics from the third century CE. The Möbius strip is a non-orientable surface, meaning that within it one cannot consistently distinguish clockwise from counterclockwise turns. Every non-orientable surface contains a Möbius strip.

As an abstract topological space, the Möbius strip can be embedded into three-dimensional Euclidean space in many different ways: a clockwise half-twist is different from a counterclockwise half-twist, and it can also be embedded with odd numbers of twists greater than one, or with a knotted centerline. Any two embeddings with the same knot for the centerline and the same number and direction of twists are topologically equivalent. All of these embeddings have only one side, but when embedded in other spaces, the Möbius strip may have two sides. It has only a single boundary curve. (Full article...)
Image 3
In graph theory, a cop-win graph is an undirected graph on which the pursuer (cop) can always win a pursuit–evasion game against a robber, with the players taking alternating turns in which they can choose to move along an edge of a graph or stay put, until the cop lands on the robber's vertex. Finite cop-win graphs are also called dismantlable graphs or constructible graphs, because they can be dismantled by repeatedly removing a dominated vertex (one whose closed neighborhood is a subset of another vertex's neighborhood) or constructed by repeatedly adding such a vertex. The cop-win graphs can be recognized in polynomial time by a greedy algorithm that constructs a dismantling order. They include the chordal graphs, and the graphs that contain a universal vertex. (Full article...)
Image 4
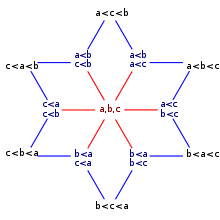
The 13 possible strict weak orderings on a set of three elements ${a, b, c$ }

In number theory and enumerative combinatorics, the ordered Bell numbers or Fubini numbers count the weak orderings on a set of $n$ elements. Weak orderings arrange their elements into a sequence allowing ties, such as might arise as the outcome of a horse race.

The ordered Bell numbers were studied in the 19th century by Arthur Cayley and William Allen Whitworth. They are named after Eric Temple Bell, who wrote about the Bell numbers, which count the partitions of a set; the ordered Bell numbers count partitions that have been equipped with a total order. Their alternative name, the Fubini numbers, comes from a connection to Guido Fubini and Fubini's theorem on equivalent forms of multiple integrals. Because weak orderings have many names, ordered Bell numbers may also be called by those names, for instance as the numbers of preferential arrangements or the numbers of asymmetric generalized weak orders. (Full article...)
Image 5

Berlin, 1959

Andrew Mattei Gleason (1921–2008) was an American mathematician who made fundamental contributions to widely varied areas of mathematics, including the solution of Hilbert's fifth problem, and was a leader in reform and innovation in mathematics teaching at all levels. Gleason's theorem in quantum logic and the Greenwood–Gleason graph, an important example in Ramsey theory, are named for him.

As a young World War II naval officer, Gleason broke German and Japanese military codes. After the war he spent his entire academic career at Harvard University, from which he retired in 1992. His numerous academic and scholarly leadership posts included chairmanship of the Harvard Mathematics Department and the Harvard Society of Fellows, and presidency of the American Mathematical Society. He continued to advise the United States government on cryptographic security, and the Commonwealth of Massachusetts on mathematics education for children, almost until the end of his life. (Full article...)
Image 6
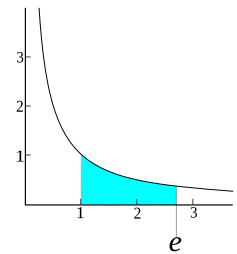
Graph of the equation $y = 1/ x$ . Here, $e$ is the unique number larger than 1 that makes the shaded area under the curve equal to 1.

The number $e$ is a mathematical constant approximately equal to 2.71828 that is the base of the natural logarithm and exponential function. It is sometimes called Euler's number, after the Swiss mathematician Leonhard Euler, though this can invite confusion with Euler numbers, or with Euler's constant, a different constant typically denoted $\gamma$ . Alternatively, $e$ can be called Napier's constant after John Napier. The Swiss mathematician Jacob Bernoulli discovered the constant while studying compound interest.

The number $e$ is of great importance in mathematics, alongside 0, 1, $π$ , and $i$ . All five appear in one formulation of Euler's identity $e^{i\pi }+1=0$ and play important and recurring roles across mathematics. Like the constant $π$ , $e$ is irrational, meaning that it cannot be represented as a ratio of integers, and moreover it is transcendental, meaning that it is not a root of any non-zero polynomial with rational coefficients. To 30 decimal places, the value of $e$ is: (Full article...)
Image 7
A polyhedron and its midsphere. The red circles are the boundaries of spherical caps within which the surface of the sphere can be seen from each vertex.

In geometry, the midsphere or intersphere of a convex polyhedron is a sphere which is tangent to every edge of the polyhedron. Not every polyhedron has a midsphere, but the uniform polyhedra, including the regular, quasiregular and semiregular polyhedra and their duals (Catalan solids) all have midspheres. The radius of the midsphere is called the midradius. A polyhedron that has a midsphere is said to be midscribed about this sphere.

When a polyhedron has a midsphere, one can form two perpendicular circle packings on the midsphere, one corresponding to the adjacencies between vertices of the polyhedron, and the other corresponding in the same way to its polar polyhedron, which has the same midsphere. The length of each polyhedron edge is the sum of the distances from its two endpoints to their corresponding circles in this circle packing. (Full article...)
Image 8
Squaring the circle: the areas of this square and this circle are both equal to $π$ . In 1882, it was proven that this figure cannot be constructed in a finite number of steps with an idealized compass and straightedge.

Squaring the circle is a problem in geometry first proposed in Greek mathematics. It is the challenge of constructing a square with the area of a given circle by using only a finite number of steps with a compass and straightedge. The difficulty of the problem raised the question of whether specified axioms of Euclidean geometry concerning the existence of lines and circles implied the existence of such a square.

In 1882, the task was proven to be impossible, as a consequence of the Lindemann–Weierstrass theorem, which proves that pi ( $\pi$ ) is a transcendental number.
That is, $\pi$ is not the root of any polynomial with rational coefficients. It had been known for decades that the construction would be impossible if $\pi$ were transcendental, but that fact was not proven until 1882. Approximate constructions with any given non-perfect accuracy exist, and many such constructions have been found. (Full article...)
Image 9
The cover page of Ars Conjectandi

Ars Conjectandi (Latin for "The Art of Conjecturing") is a book on combinatorics and mathematical probability written by Jacob Bernoulli and published in 1713, eight years after his death, by his nephew, Niklaus Bernoulli. The seminal work consolidated, apart from many combinatorial topics, many central ideas in probability theory, such as the very first version of the law of large numbers: indeed, it is widely regarded as the founding work of that subject. It also addressed problems that today are classified in the twelvefold way and added to the subjects; consequently, it has been dubbed an important historical landmark in not only probability but all combinatorics by a plethora of mathematical historians. The importance of this early work had a large impact on both contemporary and later mathematicians; for example, Abraham de Moivre.

Bernoulli wrote the text between 1684 and 1689, including the work of mathematicians such as Christiaan Huygens, Gerolamo Cardano, Pierre de Fermat, and Blaise Pascal. He incorporated fundamental combinatorial topics such as his theory of permutations and combinations (the aforementioned problems from the twelvefold way) as well as those more distantly connected to the burgeoning subject: the derivation and properties of the eponymous Bernoulli numbers, for instance. Core topics from probability, such as expected value, were also a significant portion of this important work. (Full article...)
Image 10
In mathematics, particularly algebraic topology and homology theory, the Mayer–Vietoris sequence is an algebraic tool to help compute algebraic invariants of topological spaces. The result is due to two Austrian mathematicians, Walther Mayer and Leopold Vietoris. The method consists of splitting a space into subspaces, for which the homology or cohomology groups may be easier to compute. The sequence relates the (co)homology groups of the space to the (co)homology groups of the subspaces. It is a natural long exact sequence, whose entries are the (co)homology groups of the whole space, the direct sum of the (co)homology groups of the subspaces, and the (co)homology groups of the intersection of the subspaces.

The Mayer–Vietoris sequence holds for a variety of cohomology and homology theories, including simplicial homology and singular cohomology. In general, the sequence holds for those theories satisfying the Eilenberg–Steenrod axioms, and it has variations for both reduced and relative (co)homology. Because the (co)homology of most spaces cannot be computed directly from their definitions, one uses tools such as the Mayer–Vietoris sequence in the hope of obtaining partial information. Many spaces encountered in topology are constructed by piecing together very simple patches. Carefully choosing the two covering subspaces so that, together with their intersection, they have simpler (co)homology than that of the whole space may allow a complete deduction of the (co)homology of the space. In that respect, the Mayer–Vietoris sequence is analogous to the Seifert–van Kampen theorem for the fundamental group, and a precise relation exists for homology of dimension one. (Full article...)
$Image 11 In mathematics, the harmonic series is the infinite series formed by summing all positive unit fractions: '"`UNIQ--postMath-0000000D-QINU`"' The first '"`UNIQ--postMath-0000000E-QINU`"' terms of the series sum to approximately '"`UNIQ--postMath-0000000F-QINU`"', where '"`UNIQ--postMath-00000010-QINU`"' is the natural logarithm and '"`UNIQ--postMath-00000011-QINU`"' is the Euler–Mascheroni constant. Because the logarithm has arbitrarily large values, the harmonic series does not have a finite limit: it is a divergent series. Its divergence was proven in the 14th century by Nicole Oresme using a precursor to the Cauchy condensation test for the convergence of infinite series. It can also be proven to diverge by comparing the sum to an integral, according to the integral test for convergence. (Full article...)$

Image 11
In mathematics, the harmonic series is the infinite series formed by summing all positive unit fractions:
$\sum _{n=1}^{\infty }{\frac {1}{n}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots .$

The first $n$ terms of the series sum to approximately $\ln n+\gamma$ , where $\ln$ is the natural logarithm and $\gamma \approx 0.577$ is the Euler–Mascheroni constant. Because the logarithm has arbitrarily large values, the harmonic series does not have a finite limit: it is a divergent series. Its divergence was proven in the 14th century by Nicole Oresme using a precursor to the Cauchy condensation test for the convergence of infinite series. It can also be proven to diverge by comparing the sum to an integral, according to the integral test for convergence. (Full article...)
Image 12

Turing in 1936

Alan Mathison Turing (/ˈtjʊərɪŋ/; 23 June 1912 – 7 June 1954) was an English mathematician, computer scientist, logician, cryptanalyst, philosopher and theoretical biologist. He was highly influential in the development of theoretical computer science, providing a formalisation of the concepts of algorithm and computation with the Turing machine, which can be considered a model of a general-purpose computer. Turing is widely considered to be the father of theoretical computer science.

Born in London, Turing was raised in southern England. He graduated from King's College, Cambridge, and in 1938, earned a doctorate degree from Princeton University. During World War II, Turing worked for the Government Code and Cypher School at Bletchley Park, Britain's codebreaking centre that produced Ultra intelligence. He led Hut 8, the section responsible for German naval cryptanalysis. Turing devised techniques for speeding the breaking of German ciphers, including improvements to the pre-war Polish bomba method, an electromechanical machine that could find settings for the Enigma machine. He played a crucial role in cracking intercepted messages that enabled the Allies to defeat the Axis powers in many engagements, including the Battle of the Atlantic. (Full article...)

Did you know

... that more than 60 scientific papers authored by mathematician Paul Erdős were published posthumously?
... that Ukrainian baritone Danylo Matviienko, who holds a master's degree in mathematics, appeared as Demetrius in Britten's opera A Midsummer Night's Dream at the Oper Frankfurt?
... that mathematician Daniel Larsen was the youngest contributor to the New York Times crossword puzzle?
... that Fathimath Dheema Ali is the first Olympic qualifier from the Maldives?
... that Green Day's "Wake Me Up When September Ends" became closely associated with the aftermath of Hurricane Katrina?
... that The Math Myth advocates for American high schools to stop requiring advanced algebra?
... that Fairleigh Dickinson's upset victory over Purdue was the biggest upset in terms of point spread in NCAA tournament history, with Purdue being a 23+1⁄2-point favorite?
... that people in Madagascar perform algebra on tree seeds in order to tell the future?

Did you know...

... that mathematician Paul Erdős called the Hadwiger conjecture, a still-open generalization of the four-color problem, "one of the deepest unsolved problems in graph theory"?
...that the six permutations of the vector (1,2,3) form a regular hexagon in 3d space, the 24 permutations of (1,2,3,4) form a truncated octahedron in four dimensions, and both are examples of permutohedra?
...that Ostomachion is a mathematical treatise attributed to Archimedes on a 14-piece tiling puzzle similar to tangram?
...that some functions can be written as an infinite sum of trigonometric polynomials and that this sum is called the Fourier series of that function?
...that the identity elements for arithmetic operations make use of the only two whole numbers that are neither composites nor prime numbers, 0 and 1?
...that as of April 2010 only 35 even numbers have been found that are not the sum of two primes which are each in a Twin Primes pair? ref
...the Piphilology record (memorizing digits of Pi) is 70000 as of Mar 2015?

More did you know facts

Showing 7 items out of 75

Featured pictures

Image 1Mandelbrot set, step 7, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 2Breeder, by Protious/Hyperdeath (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 3Mandelbrot set, step 1, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 4Mandelbrot set, step 14, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 5Mandelbrot set, step 3, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 6Missing square puzzle, by Fibonacci (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 7Mandelbrot set, step 4, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 8Mandelbrot set, step 6, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 9Cellular automata at Reflector (cellular automaton), by Simpsons contributor (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 10Desargues' theorem, by Dynablast (edited by Jujutacular and Julia W) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 11Non-uniform rational B-spline, by Greg L (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 12Mandelbrot set, step 5, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 13Mandelbrot set, step 2, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 14Helicatenoid, by Wickerprints (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 15Mandelbrot set, step 13, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 16Proof of the Pythagorean theorem, by Joaquim Alves Gaspar (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 17Mandelbrot set, start, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 18Mandelbrot set, step 10, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 19Fields Medal, back, by Stefan Zachow (edited by King of Hearts) (from Wikipedia:Featured pictures/Sciences/Mathematics)
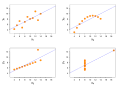
Image 20Anscombe's quartet, by Schutz (edited by Avenue) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 21Mandelbrot set, step 11, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 22Radian, by Lucas V. Barbosa (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 23Mandelbrot set, by Simpsons contributor (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 24Mandelbrot set, step 9, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 25Fields Medal, front, by Stefan Zachow (edited by King of Hearts) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 26Hypotrochoid, by Sam Derbyshire (edited by Anevrisme and Perhelion) (from Wikipedia:Featured pictures/Sciences/Mathematics)
$Image 27Lyapunov fractal, by BernardH (from Wikipedia:Featured pictures/Sciences/Mathematics)$

Image 27Lyapunov fractal, by BernardH (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 28Mandelbrot set, step 12, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 29Tetrahedral group at Symmetry group, by Debivort (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 30Line integral of scalar field, by Lucas V. Barbosa (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 31Lorenz attractor at Chaos theory, by Wikimol (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 32Mandelbulb, by Ondřej Karlík (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 33Topological knots, by Jkasd (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 34Mandelbrot set, step 8, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)

Get involved

For editor resources and to collaborate with other editors on improving Wikipedia's Mathematics-related articles, visit WikiProject Mathematics.

Categories

» Category:Mathematics, Category:People

Topics

» Lists of mathematics topics, Glossary of areas of mathematics, History of mathematics

Index of articles

ARTICLE INDEX:	0–9 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
MATHEMATICIANS:	A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Vital articles

» subpages: Level 4 Mathematics articles, Level 5 Mathematics articles

Discover Wikipedia using portals